Beispiel zum Programm Anfangswertproblem
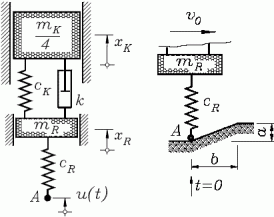 Für die Analyse der Vertikalschwingungen
eines Rades infolge der Bodenunebenheiten
und der Übertragung der Schwingungen auf
die Karosse dient das skizzierte Berechnungsmodell: Zwischen dem Rad (Masse
mR)
und der Karosserie befinden sich eine Feder und ein Dämpfungsglied
(Stoßdämpfer mit geschwindigkeitsproportionaler
Dämpfung), auf denen näherungsweise ein Viertel der
Karosseriemasse mK lastet. Die
Elastizität der Bereifung wird durch die Federzahl
cR erfasst. Dem Punkt
A wird die Vertikalbewegung
u(t) aufgezwungen.
Für die Analyse der Vertikalschwingungen
eines Rades infolge der Bodenunebenheiten
und der Übertragung der Schwingungen auf
die Karosse dient das skizzierte Berechnungsmodell: Zwischen dem Rad (Masse
mR)
und der Karosserie befinden sich eine Feder und ein Dämpfungsglied
(Stoßdämpfer mit geschwindigkeitsproportionaler
Dämpfung), auf denen näherungsweise ein Viertel der
Karosseriemasse mK lastet. Die
Elastizität der Bereifung wird durch die Federzahl
cR erfasst. Dem Punkt
A wird die Vertikalbewegung
u(t) aufgezwungen.
| Gegeben: | mK = | 1000 kg ; | cK = | 300 N/cm ; | k = | 750 kg/s ; | v0 = | 50 km/h ; |
| mR = | 25 kg ; | cR = | 900 N/cm ; | a = | 20 cm ; | b = | 40 cm . |
Es sollen die Vertikalschwingungen des Rades und der Karosserie ermittelt werden (Analyse der Bewegungen für 0 ≤ t ≤ 3 s), wenn der Punkt A zum Zeitpunkt t = 0 eine Aufwärtsbewegung auf einer geneigten Linie (rechte Skizze) beginnt und nach Erreichen der Höhe a sich horizontal weiter bewegt. Es soll angenommen werden, dass bis zum Erreichen der Höhe a eine horizontale Strecke b mit einer konstanten Geschwindigkeit v0 zurückgelegt wird, so das der Punkt A diese Strecke nach Δt = b/v0 zurückgelegt hat.
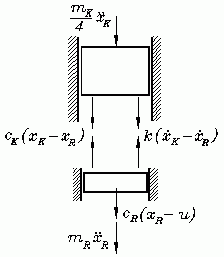
Die nebenstehende Schnittskizze gestattet die Formulierung der Bewegungs-Differenzialgleichungen (zum Beispiel mit Hilfe des Prinzips von d'Alembert):
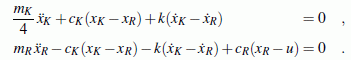
Sämtliche Anfangswerte (beide Koordinaten und ihre Ableitungen) haben den Wert 0. Das lineare Differenzialgleichungssystem kann mit erträglichem Aufwand nur numerisch gelöst werden, weil die Funktion u(t) das Problem erheblich erschwert. Für diese Funktion gilt:
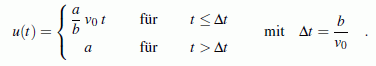
Das Anfangswertproblem 2. Ordnung kann durch Einführen zweier neuer Variablen vK und vR für die ersten Ableitungen von xK bzw. xR in ein Anfangswertproblem 1. Ordnung überführt werden, das in dieser Form dem Programm "Anfangswertproblem" angeboten werden kann:
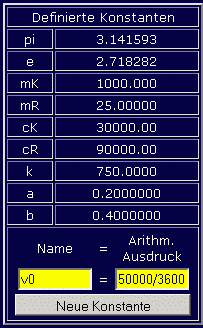
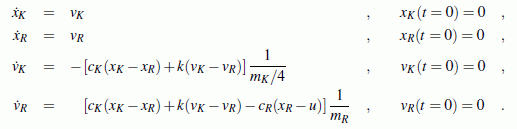
Nach dem Start des Programms "Anfangswertproblem" werden zunächst die gegebenen Parameter als Konstanten definiert, die alle auf die Dimensionen kg, m, s und N umgerechnet wurden. Rechts sieht man die Tabelle mit den beiden vordefinierten Konstanten pi und e und den bereits definierten Konstanten mK, mR, cK, cR, k, a und b. Im gelben Bereich sieht man die Vorbereitung der Definition von v0, und nach Klick auf "Neue Konstante" ist die Konstantendefinition abgeschlossen.
Von den Voreinstellungen für den Integrationsbereich (tanf, tend, nsteps) muss nur tend auf den Wert 3 geändert werden. Das Problem mit der Funktion u(t) wird gelöst, indem eine Funktion u als Summe der beiden Funktionen u1 und u2 definiert wird, wobei der Gültigkeitsbereich von u1 auf t ≤ b/v0 beschränkt wird und u2 erst ab t > b/v0 gilt (außerhalb der Gültikeitsbereiche haben die Funktionen den Wert 0). Wenn u1 in das Feld "Name" eingetragen wird, bietet das Programm im rechten Bereich dieser Zeile das Schema für die Eingabe des Gültigkeitsbereichs an. Nach Eintragen des erweiterten arithmetischen Ausdrucks (in diesem Fall: a/b*v0*t) und des Gültigkeitsbereichs sieht die Eingabezeile so aus:

Nach Anklicken von "OK" können die anderen Funktionen und Differenzialgleichungen definiert werden. Für die Definition der Differenzialgleichungen muss im Eingabefeld der Funktionsname jeweils mit dem Zeichen ' ergänzt werden. Dann wird zusätzlich die Anfangsbedingung abgefragt. Für die letzte der Differenzialgleichungen sieht die komplett ausgefüllte Eingabezeile so aus:

Alle Eingaben werden unterhalb des Eingabebereichs protokolliert. Vor der Berechnung sollte immer das Angebot "Syntaxcheck" genutzt werden. Nach Anklicken des entsprechenden Buttons sieht das Eingabeprotokoll so aus:

Nun kann der Button "Berechnung starten" angeklickt werden. Als Ergebnisse erscheinen zunächst die vier Funktionen, die als Lösungen der vier Differenzialgleichungen ermittelt wurden, in einem Diagramm:
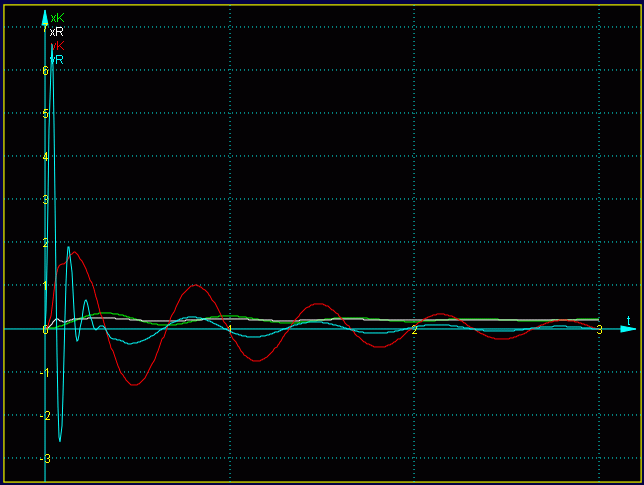
Das ist natürlich etwas unübersichtlich und wird nachfolgend noch verbessert. Zunächst aber soll überprüft werden, ob man den Ergebnissen vertrauen kann. Man sollte grundsätzlich mindestens eine zweite Rechnung mit einer größeren Schrittanzahl durchführen und die Endwerte vergleichen, die im Programm gesammelt werden. Nachfolgend sieht man diese Werte für insgesamt 4 Rechnungen mit unterschiedlicher Schrittanzahl:
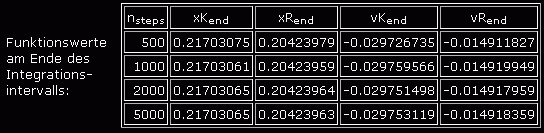
Die Werte ändern sich nur unbedeutend. Selbst die erste Rechnung mit nsteps = 500 genügt auch gehobenen Genauigkeitsanforderungen.
Zur Verbesserung der grafischen Darstellung steht unterhalb der Grafik ein blaues Feld zur Verfügung, in dem die gewünschten Parameter eingestellt werden können. Zuächst wird die Anzahl der Grafikfenster (Standardeinstellung: 1) auf 4 erhöht (1, 2 oder 4 sind möglich). Das blaue Feld erweitert sich entsprechend, folgende Änderungen werden vorgenommen: Im Grafikfenster 1 (links oben) sollen nur noch die Wegkoordinaten xK und xR dargestellt werden, zusätzlich die Funktion u, im Grafikfenster 3 (links unten) die Geschwindigkeiten vK und vR, was jeweils durch entsprechende Änderung im Eingabefeld "Funktionen" realisiert wird. Im Graphikfenster 2 (rechts oben) soll vK in Abhängigkeit von xK dargestellt werden, dafür müssen im Feld "Funktionen" vK und im Feld "Abszisse" xK eingetragen werden (Standard ist t). Im Grafikfenster 4 schließlich sollen xK, xR und u für eine kürzeren Zeitbereich gezeigt werden, um die Reaktion der Karosse unmittelbar beim Überfahren der Schwelle zu verdeutlichen. Nachdem auch noch einge sinnvolle Änderungen für die Raster der einzelnen Fenster vorgenommen wurden, sieht das blaue Feld zum Beispiel so aus:
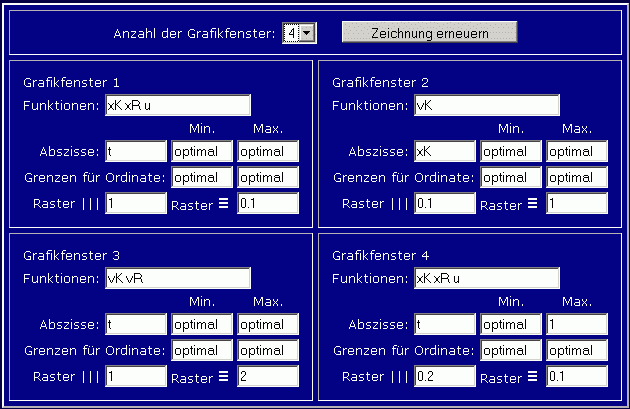
Nach Anklicken des Buttons "Zeichnung erneuern" sieht die Grafik so aus:
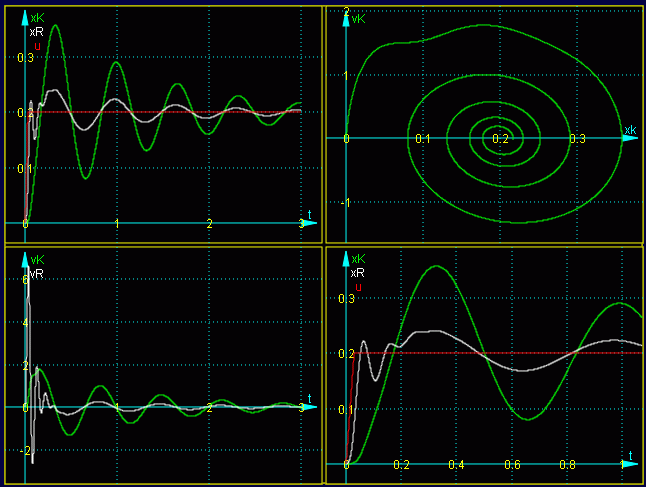
Die Grafik unten rechts (Fenster 4) zeigt den interessanten Verlauf der Bewegung von Rad und Karosse: Währen die Bewegung des Rades (Koordinate xR) der Schwelle (Koordinate u) ziemlich direkt folgt, schwingt die Karosse (Koordinate xK) zunächst ziemlich weit aus und hat sich erst nach einigen Sekunden auf das erhöhte Niveau eingeschwungen (der typische alte amerikanische "Straßenkreuzer"). Diese Bewegung wird auch sehr schön durch die so genannte "Darstellung in der Phasenebene" (rechts oben) deutlich: Die Kurve "umkreist den Ruhepunkt" xK = 0,2 bei vK = 0 und nähert sich diesem dabei relativ langsam.