Beispiel zum Programm Anfangswertproblem
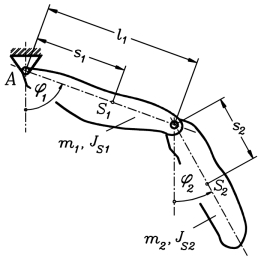
Ein Doppelpendel wird definiert durch die beiden Pendelmassen m1 und m2, die auf die jeweiligen Schwerpunkte bezogenen Massenträgheitsmomente JS1 und JS2, die Schwerpunktabstände von den Drehpunkten s1 und s2 und den Abstand l1 der beiden Drehpunkte voneinander.
Die Bewegung soll durch die Funktionen φ1(t) und φ2(t) beschrieben werden, die für das Zeitintervall t = 0 ... 10 s zu berechnen sind.
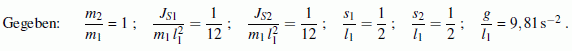
Die Aufgabe wird im Lehrbuch "Dankert/Dankert: Technische Mechanik" in den Kapiteln "Prinzipien der Mechanik" (Aufschreiben der Bewegungs-Differenzialgleichungen) und "Verifizieren von Computerrechnungen" (Diskussion der Ergebnisse) behandelt.
Die gegebenen Werte gelten für zwei schlanke Stäbe gleicher Masse und gleicher Länge. Sie sollen aus der nebenstehend skizzierten Anfangslage ohne Anfangsgeschwindigkeiten freigelassen werden, so dass folgende Anfangsbedingungen gelten:
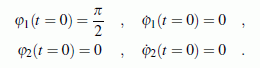
Im oben genannten Lehrbuch wird die (nicht ganz einfache) Herleitung der Bewegungs-Differenzialgleichungen ausführlich beschrieben. Unter Verwendung der in der Aufgabenstellung skizzierten Koordinaten erhält man:
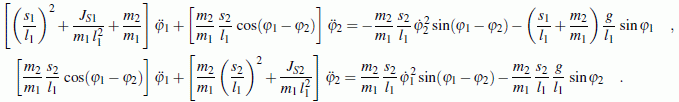
Das Programm "Anfangswertproblem" erwartet ein Differenzialgleichungssystem 1. Ordnung. Deshalb werden die beiden neuen Variablen ω1 und ω2 eingeführt:
Damit kann das Anfangswertproblem so formuliert werden, wie man es (fast) dem Programm "Anfangswertproblem" anbieten kann:
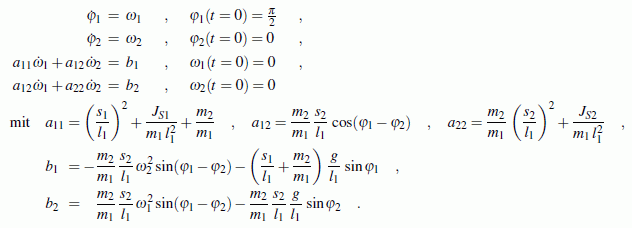
Bleibt nur noch das Problem, dass das Programm "Anfangswertproblem" die nach den ersten Ableitungen aufgelösten Differenzialgleichungen erwartet. Die 3. und 4. Differenzialgleichung bilden ein einfaches lineares Gleichungssystem, dessen Lösung man zum Beispiel sofort nach der Cramerschen Regel aufschreiben kann, so dass man schließlich diese vier Differenzialgleichungen hat:
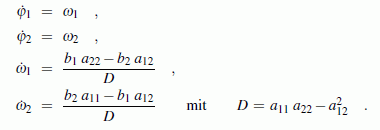
Nach dem Start des Programms "Anfangswertproblem" werden zunächst die gegebenen Parameter als Konstanten definiert. Rechts sieht man die Tabelle mit den beiden vordefinierten Konstanten pi und e und den zusätzlich definierten dimensionslosen Parametern m2dm1 ("m2 durch m1"), J1, J2, s1, s2 und dem einzigen dimensionsbehafteten Wert gdl ("g durch l"), der die Dimension s für die Zeit in die Ergebnisse überträgt.
Die Voreinstellungen für den Integrationsbereich (tanf, tend, nsteps) werden nicht verändert, obwohl zu vermuten ist, dass die voreingestellte Anzahl der Integrationsschritte nsteps = 500 für die komplizierte Bewegung eines Doppelpendels nicht genügen wird. Aber man muss ohnehin mehrfach rechnen. Zunächst werden die Funktionen, mit denen die Differenzialgleichungen beschrieben werden, eingegeben, zum Beispiel:

Zu jeder Funktion gehört ein Gültigkeitsbereich, für den allerdings hier immer die Standardvorgabe (t ≥ 0, gültig im gesamten Integrationsbereich) übernommen werden kann. Bei der Eingabe einer Differenzialgleichung (vom Programm wird dies daran erkannt, dass im Eingabefeld "Name" der Funktionsname jeweils mit dem Zeichen ' ergänzt werden muss) wird die zugehörige Anfangsbedingung abgefordert. Das sieht zum Beispiel so aus:

Alle Eingaben werden unterhalb des Eingabebereichs protokolliert. Wenn alle Funktionen und Differenzialgleichungen eingegeben sind, sollte vor der Berechnung immer das Angebot "Syntaxcheck" genutzt werden. Nach Anklicken des entsprechenden Buttons sieht das Eingabeprotokoll so aus:
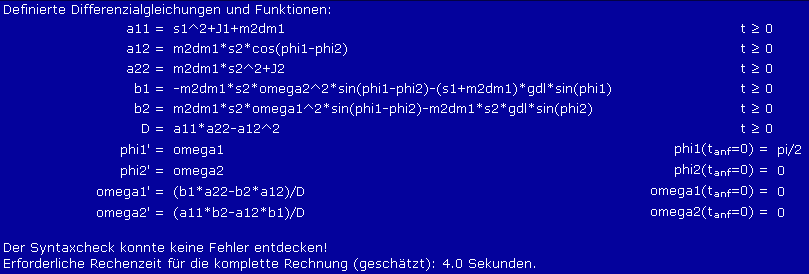
Nun kann der Button "Berechnung starten" angeklickt werden. Als Ergebnisse erscheinen zunächst die Zahlenwerte am Ende des Berechnungsintervalls für die vier Funktionen, die als Lösungen der vier Differenzialgleichungen ermittelt wurden, und die grafische Darstellung dieser Funktionen über das gesamte Berechnungsintervall in einem Diagramm:
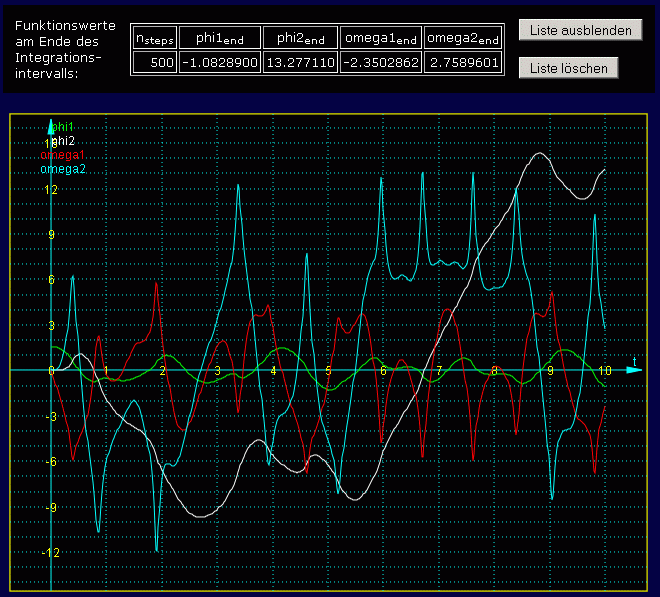
Das ist natürlich etwas unübersichtlich und wird nachfolgend noch verbessert. Zunächst aber muss überprüft werden, ob man den Ergebnissen vertrauen kann. Man sollte grundsätzlich mindestens eine zweite Rechnung mit einer größeren Schrittanzahl durchführen und die Endwerte vergleichen, die im Programm gesammelt werden. Schon die erste Rechnung mit größerer Schrittanzahl weicht deutlich von den ersten Ergebnissen ab, so dass noch weiter verfeinert wird. Nachfolgend sieht man die Werte am Ende des Berechnungsintervalls für insgesamt 4 Rechnungen mit unterschiedlicher Schrittanzahl:
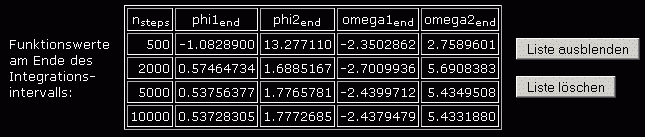
Die Werte für die beiden Rechnungen mit mit nsteps = 5000 und nsteps = 10000 weichen nur unbedeutend voneinander ab, so dass man ihnen vertrauen kann. Trotzdem soll noch eine zusätzliche Kontrolle realisiert werden, die bei diesem System, bei dem keine Energieverluste während der Bewegung berücksichtigt wurden, sehr effektiv ist. Die Summe aus potenzieller und kinetischer Energie kann für einen beliebigen Zeitpunkt der Bewegung so formuliert werden (das Nullpotenzial für die potenzielle Energie wurde auf dem Niveau des Lagerpunktes angenommen):
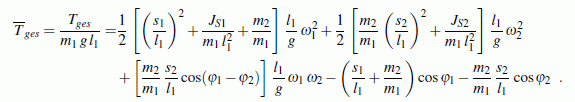
Weil mit den gegebenen Größen weitgehend dimensionslos gerechnet wurde, ist auch die Energie dimensionslos aufgeschrieben worden. Dieser etwas monströs aussehende Ausdruck muss für jeden Satz der Bewegungsgrößen φ1(t), φ2(t), ω1(t) und ω2(t) den gleichen Wert ergeben. Es ist die Gesamtenergie, die bereits am Anfang der Bewegung (als potenzielle Energie) vorhanden war:
Diese Funktion wird zusätzlich eingegeben. Das erweiterte Eingabeprotokoll sieht dann so aus:

Nach erneutem Anklicken des Buttons "Berechnung starten" ändert sich an der Ergebnisanzeige zunächst nichts. Die Werte für die zusätzliche Funktion werden zwar berechnet, automatisch angezeigt werden aber nur Ergebnisse der Integration der Differenzialgleichungen. Zur individuellen Einstellung der grafischen Darstellung steht unterhalb der Grafik ein blaues Feld zur Verfügung, in dem die gewünschten Parameter eingestellt werden können. Zuächst wird die Anzahl der Grafikfenster (Standardeinstellung: 1) auf 4 erhöht (1, 2 oder 4 sind möglich). Das blaue Feld erweitert sich entsprechend, folgende Änderungen werden vorgenommen: Im Grafikfenster 1 (links oben) soll nur noch die Winkelkoordinate phi1, darunter im Grafikfenster 3 die Winkelkoordinate phi2 dargestellt werden, was jeweils durch entsprechende Änderung im Eingabefeld "Funktionen" realisiert wird. Im Graphikfenster 2 (rechts oben) sollen die beiden Winkelgeschwindigkeiten omega1 und omega2 dargestellt werden (im Eingabefeld "Funktionen" müssen die beiden Namen durch Leerzeichen getrennt werden). Im Grafikfenster 4 schließlich soll Tq_ges dargestellt werden. Nachdem auch noch einige sinnvolle Änderungen für die Raster der einzelnen Fenster vorgenommen wurden, sieht das blaue Feld zum Beispiel so aus:
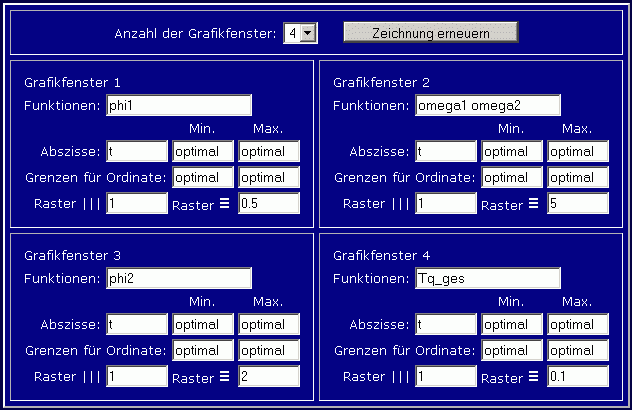
Nach Anklicken des Buttons "Zeichnung erneuern" sieht die Grafik so aus:
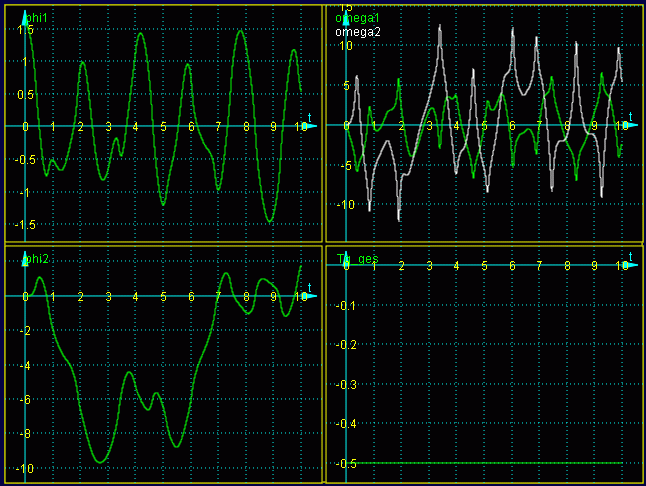
Die Kontrollfunktion (unten rechts) zeigt tatsächlich den erwarteten konstanten Wert -0.5 über den gesamten Zeitbereich und ist damit ein gutes Indiz für die Qualität der Rechnung, natürlich auch eine Bestätigung dafür, dass die komplizierten Funktionen mit großer Wahrscheinlichkeit korrekt eingegeben wurden.
Die recht bizarren Funktionsverläufe spiegeln den tatsächlich außerordentlich komplizierten Bewegungsablauf eines solchen Doppelpendels wider. Während das obere Pendel (Funktion phi1) eine recht unregelmäßige Schwingung ausführt, beginnt das untere Pendel (Funktion phi2) mit einem "Salto", dem bald darauf ein "Salto rückwärts" folgt. Hier findet man eine Animation der Bewegung, die das sehr anschaulich zeigt. Hier findet man einen Wegweiser zur Berechnung dieser Aufgabe mit verschiedenen anderen Programmen und Verfahren.