Ebene Starrkörpersysteme als Fachwerke
|
Ein aus drei (starren) Fachwerkstäben gebildetes Dreieck ist ein starrer Körper. Wenn an ein solches Dreieck ein weiteres Dreieck aus genau zwei neuen Stäben und einem neuen Knoten angefügt wird, entsteht ein so genanntes "Fachwerk mit einfachem Aufbau", das auch ein Starrkörpersystem ist. Es ist also möglich, jedes statisch bestimmte Starrkörpersystem als Fachwerk zu modellieren, und dieses dann mit Hilfe eines Programms zur Berechnung von statisch bestimmten Fachwerken zu berechnen. Die Ergebnisse sind im Sinne der Statik exakt. Dies wird nachfolgend an mehreren Beispielen demonstriert. |
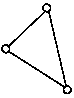 Dreieck aus 3 Fachwerk-Stäben |
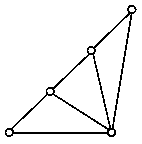 Jedes zusätzliche Dreieck muss genau einen neuen Knoten und zwei neue Stäbe erzeugen |
||||
|
Folgende Vorgehensweise wird empfohlen:
|
||||||
| Beispiel 1: | ||||||
|
||||||
|
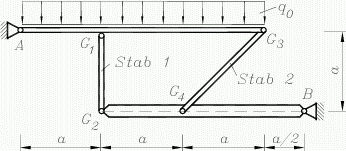
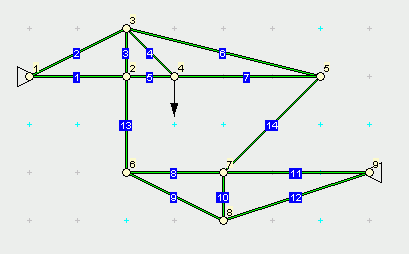
Rechts sieht man das Ergebnis: Die beiden Stäbe sind Stäbe geblieben, die beiden Festlager haben sich auch nicht verändert. Der obere Träger hat vier markante Punkte (Festlager, zwei Anschlussstellen der Stäbe und den Angriffspunkte der Linienlast), der untere Träger nur drei markante Punkte. Diese sind jeweils die Ausgangspunkte für die zu erzeugenden Dreiecke. Dieses System wurde online interaktiv mit dem Applet zur Berechnung von statisch bestimmten Fachwerken modelliert und berechnet. Der nachfolgende Bildschirm-Schnappschuss zeigt das Ergebnis (die Werte können mit der Rechnung mit den Gleichgewichtsbedingungen der Statik verglichen werden): 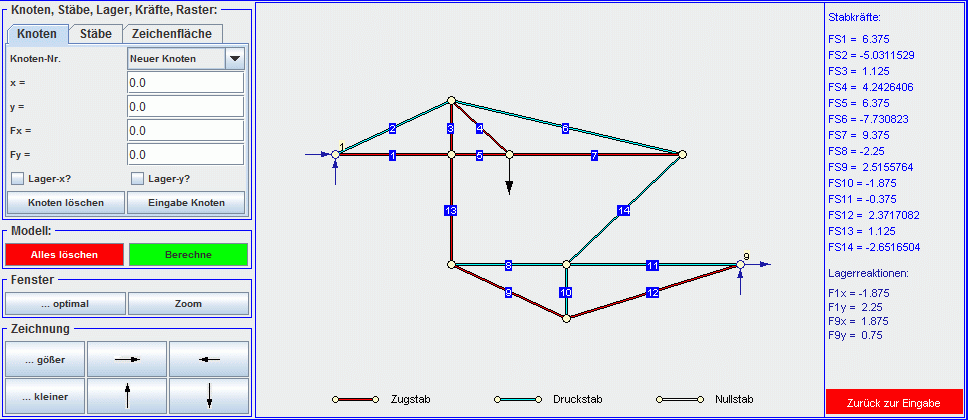 |
||||||
|
Beispiel 2: |
||||||
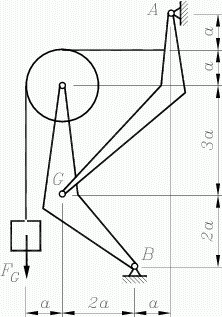
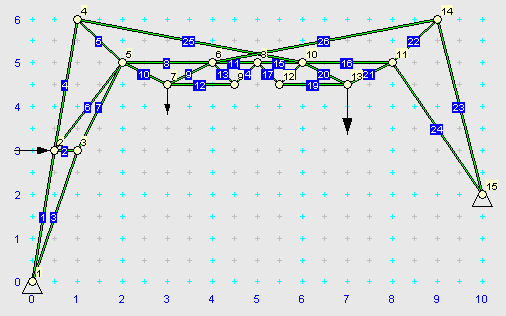
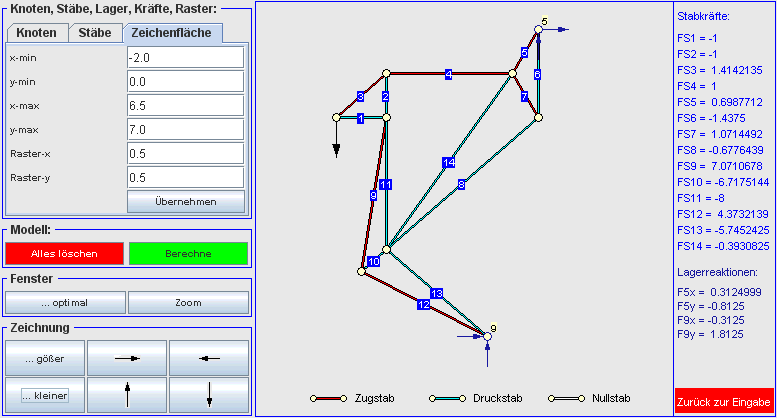
Das links dargestellte Starrkörpersystem (entnommen aus dem Kapitel "Systeme starrer Körper") soll als Fachwerk modelliert werden. Rechts sieht man das Ergebnis: Die Umlenkrolle wurde als ein Stab-Dreieck modelliert, die beiden anderen Starrkörper mit zwei Dreiecken. Es wurden einige Stäbe mehr als unbedingt erforderlich modelliert, um dem System eine gewisse optische Ähnlichkeit mit dem Original zu erhalten. Dieses System wurde online interaktiv mit dem Applet zur Berechnung von statisch bestimmten Fachwerken modelliert und berechnet. Der nachfolgende Bildschirm-Schnappschuss zeigt das Ergebnis (die Werte können mit der Rechnung mit den Gleichgewichtsbedingungen der Statik verglichen werden): |
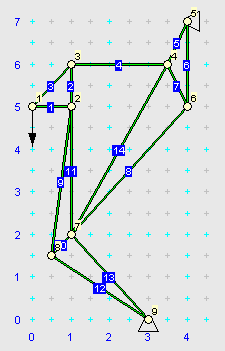
|
|||||
 |
||||||
|
Beispiel 3: |
||||||
|
||||||
|
Rechts sieht man das Ergebnis: Die beiden Seile sind zu Stäben geworden, die beiden Festlager haben sich auch nicht verändert. Der Starrkörper rechts wurde durch ein Dreieck ersetzt, die drei anderen Starrkörper durch jeweils drei Dreiecke. Es wurden einige Stäbe mehr als unbedingt erforderlich modelliert, um dem System eine gewisse optische Ähnlichkeit mit dem Original zu erhalten. Dieses System wurde online interaktiv mit dem Applet zur Berechnung von statisch bestimmten Fachwerken modelliert und berechnet. Der nachfolgende Bildschirm-Schnappschuss zeigt das Ergebnis (die Werte können mit der Rechnung mit den Gleichgewichtsbedingungen der Statik verglichen werden): 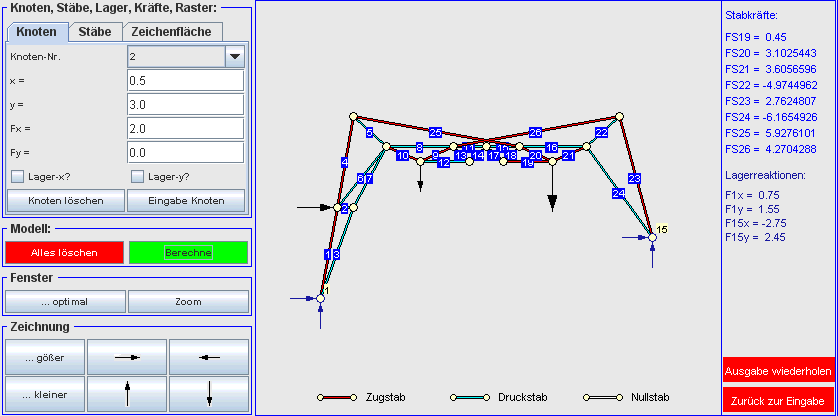 |
||||||