Nachfolgend sind die wichtigsten Informationen zur Bedienung des Programms alphabetisch zusammengestellt. Bei Klick auf die unterstrichenen hellblauen Stichworte öffnet sich jeweils ein Fenster mit ausführlichen Zusatzinformationen.

Allgemeines Matrizeneigenwertproblem --> Spezielles Matrizeneigenwertproblem (nur für Interessenten, Information ist für die Benutzung des Programms nicht erforderlich): Wenn ein allgemeines Matrizeneigenwertproblem (A - λ B) x = o mit symmetrischen Matrizen A und B berechnet werden soll, so wird dieses zunächst auf ein spezielles Eigenwertproblem mit folgender Strategie reduziert:

Die Matrix B wird nach Cholesky in das Produkt B = R^TR zerlegt. Die Rechtsdreiecksmatrix R wird invertiert, und das allgemeine Matrizeneigenwertproblem wird von links mit (R^T)⁻¹ multipliziert und R wird nach rechts ausgeklammert. Es entsteht das spezielle Matrizeneigenwertproblem (A^* − λ E) x^* = o mit der Matrix A^* = (R^T)⁻¹AR⁻¹, die wie A symmetrisch ist und die gleichen Eigenwerte hat. Dieses "reduzierte" Matrizeneigenwertproblem wird nach Jacobi gelöst. Die berechneten Eigenvektoren müssen entsprechend x = R⁻¹x^* rücktransformiert werden.

Dieser Weg funktioniert nur, wenn die Matrix B positiv definit ist (siehe Seite "Positiv definit", was ist das?), weil sonst die Cholesky-Zerlegung misslingt. In diesem Fall wird versucht, die Matrix A nach Cholesky zu zerlegen. Wenn dies gelingt, wird (analog zur oben beschriebenen Strategie) das inverse spezielle Matrizeneigenwertproblem erzeugt, das die reziproken Eigenwerte liefert, die entsprechend zurückgerechnet werden müssen. Erst dann, wenn auch dieser Weg erfolglos ist, wird die Rechnung mit der Ausschrift "Beide Matrizen (A und B) sind nicht positiv defint" beendet.

Von dem gesamten Algorithmus, der hier beschrieben wurde, merkt der Programmbenutzer nichts.

Die Ergebnisse der Arcusfunktionen asin, acos, atan und acot können in Grad (°) oder Radian (Bogenmaß) abgeliefert werden. Dies wird über die Radiobuttons eingestellt (Standardeinstellung ist Grad, siehe nebenstehendes Bild).

Ein Arithmetischer Ausdruck darf Zahlen, öffnende und schließende Klammern ([{}]), die Symbole für die vier Grundrechenarten + - * / und das Potenzieren ^, die Namen bereits definierter Konstanten und Standardfunktionen (mit Argumenten in Klammern) enthalten. Hier findet man ausführlichere Informationen und Beispiele.

Als Berechnungsverfahren wird das Rotationsverfahren von Jacobi verwendet (ausführlich beschrieben im Bereich "Mathematik für die Technische Mechanik" auf der Seite "Das Verfahren von Jacobi"). Es arbeitet iterativ, indem mit Hilfe von elementaren Orthogonaltransformationen (so genannten "Jacobi-Rotationen") die Matrix A des speziellen Matrizeneigenwertproblems sukzessive in eine Diagonalmatrix überführt wird, die dann als Diagonalelemente die Eigenwerte von A enthält. Das Produkt aller elementaren Orthogonalmatrizen enthält spaltenweise die zugehörigen Eigenvektoren.

Der Fehler der berechneten Eigenwerte wird in jedem Schritt über die Summe der Quadrate der Nichtdiagonalelemente der geänderten Matrix A abgeschätzt. Die Rechnung wird beendet, wenn entweder die vorgegebene Genauigkeit erreicht oder die vorgegebene maximale Anzahl von Jacobi-Rotationen überschritten wurde.

Das allgemeine Matrizeneigenwertproblem wird nach dem gleichen Verfahren gelöst, nachdem es vorher unter Erhalt der Symmetrie in ein spezielles Matrizeneigenwertproblem überführt wurde (siehe "Allgemeines Matrizeneigenwertproblem --> Spezielles Matrizeneigenwertproblem").

Als Eingabeschema kann "... spezielles Matrizeneigenwertproblem" oder "... allgemeines Matrizeneigenwertproblem" gewählt werden, und mit dem Eintrag in das Feld "Zeilen-/Spalten-Anzahl der Matrizen n = " legt man die Dimension der Matrizen fest. Dies sind die Voreinstellungen beim Programmstart, die dem aktuellen Problem anzupassen sind:

Wenn man das Eingabeschema "... spezielles Matrizeneigenwertproblem" wählt, sind nur die Elemente des rechten oberen Dreiecks der Matrix A für die Eingabe zugänglich (alle anderen Felder sind "gegraut"). Die Eingabe eines Matrixelements (Zahl oder arithmetischer Ausdruck) wird mit der Enter- oder der Tab-Taste abgeschlossen, dabei springt der Fokus automatisch auf das nächste Eingabefeld (man kann natürlich auch mit Mausklick ein beliebiges Feld ansteuern). Nach Eingabe eines Elements wird automatisch das zugehörige "Symmetrie-Element" im linken unteren Dreieck der Matrix auf den gleichen Ausdruck geändert, so dass immer eine symmetrische Matrix zu sehen ist.

Die Matrix B ist beim speziellen Matrizeneigenwertproblem die Einheitsmatrix und kann deshalb im Eingabeschema nicht geändert werden. Ein komplett ausgefülltes Eingabeschema kann zum Beispiel so aussehen (siehe Beispiel "Hauptträgheitsmomente und Hauptzentralachsen"):

Wenn das Eingabeschema "... allgemeines Matrizeneigenwertproblem" gewählt wird, gelten alle oben gemachten Aussagen zusätzlich für die Eingabe der Matrix B. Ein komplett ausgefülltes Eingabeschema kann zum Beispiel so aussehen (siehe Beispiel "Torsionseigenschwingungen eines Getriebes"):

Als Ergebnisse werden grundsätzlich zunächst die Eigenwerte in geordneter Form ausgewiesen (die kleinsten zuerst). Diese Reihenfolge entspricht nicht der Anordnung auf der Hauptdiagonalen der transformierten Matrix, wo sie in ungeordneter Form entstehen.

Bei Bedarf können zusätzlich die Eigenvektoren nachgefordert werden, die in der Reihenfolge ausgegeben werden, die mit der Ausgabe der Eigenwerte korrespondiert (x₁ ist der Eigenvektor zum kleinsten Eigenwert λ₁). Die Eigenvektoren sind grundsätzlich normiert, so dass (auch beim allgemeinen Matrizeneigenwertproblem) x_i^Tx_i = 1 gilt.

Grad/Radian, siehe Winkelfunktionen bzw. Arcusfunktionen.

Der Fehler, mit dem die berechneten Eigenwerte behaftet sind, wird wie folgt abgeschätzt: Bei der sukzessiven Transformation der Matrix A wird ständig die "Summe der Quadrate der Nichtdiagonalelemente" berechnet. Die Quadratwurzel aus dieser Summe ist eine obere Grenze für den absoluten Fehler der berechneten Eigenwerte (siehe "Das Verfahren von Jacobi"). Das Verfahren wird abgebrochen, wenn dieser Wert kleiner ist als der vorgegebene zulässige Fehler, für den die oben rechts zu sehenden Voreinstellungen vorgesehen sind (können bei Bedarf geändert werden).

Der tatsächlich erreichte Wert für die obere Fehlergrenze wird nach der Rechnung ausgewiesen (nebenstehendes Bild). Weil die Fehlerabschätzung im Programm eher vorsichtig erfolgt, ist in der Regel der Fehler der berechneten Eigenwerte noch kleiner.

Eine Jacobi-Rotation ist eine elementare Ähnlichkeitstransformation einer symmetrischen Matrix mit dem Ziel, ein Nichtdiagonal-Element der Matrix zu Null zu machen. Das Jacobi-Verfahren arbeitet mit einer Sequenz solcher Transformationen mit dem Ziel, alle Nichtdiagonal-Elemente sehr klein werden zu lassen, so dass schließlich die Ähnlichkeitstransformation erreicht wird, aus der sich Eigenwerte und Eigenvektoren ablesen lassen. Ausführliche Informationen findet man im Bereich "Mathematik für die Technische Mechanik" auf den Seiten "Jacobi- und Givens-Rotationen", "Das Verfahren von Jacobi" und "Symmetrische Matrizeneigenwertprobleme".

Jacobi-Verfahren, siehe Berechnungsverfahren

Konstanten können über die gelben Eingabefelder (links oben) definiert werden (siehe nebenstehendes Bild). Die Definition muss mit Klick auf den Button "Neue Konstante" abgeschlossen werden. Der Wert des arithmetischen Ausdrucks wird berechnet, und die Konstante wird mit Namen und Wert im Konstantenspeicher für die weitere Verwendung bereitgestellt. Der Wert einer Konstanten kann geändert werden, indem eine Konstante gleichen Namens noch einmal definiert wird.

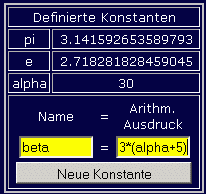
Das nebenstehende Beispiel zeigt die beiden beim Programmstart vordefinierten Konstanten pi (Kreiszahl π) und e (Basis der natürlichen Logarithmen), eine bereits zusätzlich definierte Konstante alpha sowie die Vorbereitung für die Definition einer weiteren Konstanten mit dem Namen beta. Nach Klick auf "Neue Konstante" wird der arithmetische Ausdruck berechnet, und es entsteht eine neue Konstante beta mit dem Wert 105.

Sollte später für alpha ein neuer Wert eingegeben werden, passt natürlich der Wert von beta nicht mehr dazu, siehe dazu "Neuberechnung der Konstanten".

Maximale Anzahl der Jacobi-Rotationen ist eines von zwei Abbruchkriterien (rechts sieht von die Voreinstellungen). Die Voreinstellung sollte eigentlich für alle Probleme ausreichend sein. Wenn nicht, dann kann der Wert erhöht werden. Jedoch sind auch dann, wenn die vorgegebene Genauigkeit der Eigenwerte nicht erreicht wurde (weil wegen Erreichens der maximalen Anzahl der Jacobi-Rotationen abgebrochen wurde), die Ergebnisse unter Umständen brauchbar. Die tatsächlich erreichte Genauigkeit wird ausgewiesen, und man muss dann entscheiden, ob diese akzeptabel ist oder eine neue Rechnung mit mehr zulässigen Jacobi-Rotationen gestartet werden soll.

Ein Name darf Buchstaben, Ziffern und den Unterstrich enthalten und muss mit einem Buchstaben beginnen, zum Beispiel: Alpha, y, x3, Laenge, v_gesamt. Es wird NICHT zwischen Groß- und Kleinbuchstaben unterschieden (PI, pi, Pi oder pI sind gleichwertig). Die Umlaute und das ß sind nicht erlaubt. Jede Konstante muss durch einen eindeutigen Namen zu identifizieren sein.

Neuberechnung der Konstanten ist angezeigt, wenn für eine bereits definierte Konstante der Wert geändert wird, weil andere Konstanten möglicherweise bei ihrer Definition diese Konstante verwendet haben können.

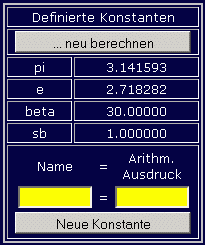
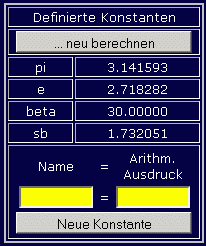
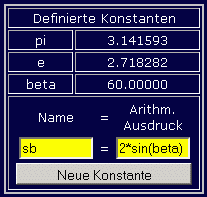
Die nebenstehenden Bildchen zeigen dies am Beispiel: Eine bereits definierte Konstante beta wird für die nachfolgende Definition der Konstanten sb verwendet (linkes Bild). Wenn nun die Konstante beta einen neuen Wert erhält (mittleres Bild), dann erscheint oben der Button "... neu berechnen", weil nun der Wert von beta nicht mehr zum berechneten Wert von sb passt. Nach Anklicken dieses Buttons "passt wieder alles zueinander" (rechtes Bild).

Nicht positiv definit, siehe "Positiv definit".

Radian/Grad, siehe Winkelfunktionen bzw. Arcusfunktionen.

Positiv definit muss mindestens eine der beiden Matrizen A und B sein. Dies ist einerseits eine Einschränkung der mit dem Programm lösbaren Probleme, andererseits sind korrekte Matrizen in der technischen Praxis (insbesondere bei Problemen der Technischen Mechanik) fast immer positiv definit, so dass mit dieser vermeintlichen Einschränkung eine starke Kontrollmöglichkeit gegeben ist, ob das Matrizeneigenwertproblem korrekt formuliert wurde.

Ausführliche Informationen findet man im Bereich "Mathematik für die Technische Mechanik)" auf der Seite "Positiv definit", was ist das?). Dort werden auch die Ursachen besprochen, die zu nicht positiv definiten Matrizen führen.

Standardfunktionen werden auf ein Argument angewendet, das der Funktionsbezeichnung in Klammern folgen muss, zum Beispiel: sin(pi/2). Das Argument darf ein arithmetischer Ausdruck sein. Hier findet man eine komplette Liste aller Standardfunktionen.

Einem Syntaxcheck werden alle Benutzer-Eingaben unterzogen. Beim Entdecken eines Fehlers wird die Abarbeitung des Programms mit einer Fehlerausschrift unterbrochen.

Die Argumente der Winkelfunktionen sin, cos, tan und cot können in Grad (°) oder Radian (Bogenmaß) interpretiert werden. Dies wird über die Radiobuttons eingestellt (Standardeinstellung ist Grad, siehe nebenstehendes Bild).

Zahlen können (optional) ein Vorzeichen, einen Dezimalpunkt und einen Exponenten (gegebenenfalls auch mit einem Vorzeichen) enthalten, Beispiele korrekter Zahlen:     -2.1E-5     5120     .3125     0.001