Biege- und dehnsteife ebene Rahmen (FEM)

Für das skizzierte Fachwerk sind Vergleichsrechnungen durchzuführen: Die Theorie des idealen Fachwerks (reibungsfreie Gelenke, Stäbe nehmen nur Zug- bzw. Druckkräfte auf) ist mit der (im Allgemeinen realen) Ausführung des Tragwerks mit biegesteifen Verbindungen (Knotenbleche) zu vergleichen. Alle Stäbe bzw. Biegeträger haben den gleichen Rechteckquerschnitt mit der Breite b und der Höhe h.

Gegeben:  a = 0,5 m ;    F = 10 kN ;    E = 2,1·10⁵ N/mm² ;
   b = 1,5 cm ;    h = 2 cm .

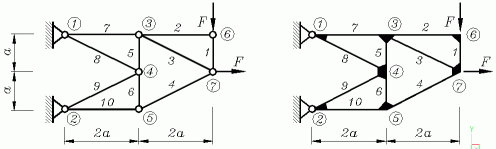
Für das Fachwerk ist eigentlich das Java-Applet "Statisch unbestimmte ebene Fachwerke (FEM)" zuständig. Das biegesteife Tragwerk wird mit dem Applet "Biege- und dehnsteife ebene Rahmen (FEM)" gelöst. Weil dieses aber auch gelenkige Verbidungen zwischen den biegesteifen Elementen zulässt, ist der Aufwand geringer, wenn das biegesteife System zunächst berechnet und danach durch Ersetzen aller Knoten durch Gelenke quasi zum idealen Fachwerk wird. Dieser Weg wird nachfolgend demonstriert.

1. Festlegen der Dimensionen für Länge und Kraft (müssen einheitlich sein für alle Eingabewerte, die Ergebnisse erhält man dann auch in den gewählten Dimensionen). Wenn man sich für mm und N entscheidet, werden folgende Eingabewerte verwendet:
   
   a = 500 mm ;    F = 10000 N ;    Dehnsteifigkeit EA = E·b·h = 6,3·10⁷ N ;    Biegesteifigkeit EI = E·b·h³/12 = 2,1·10⁹ Nmm² .
   
   Die Werte für Dehnsteifigkeit und Biegesteifigkeit können in das Programm zum Beispiel als 6.3e7 bzw. 2.1e9 eingegeben werden
   
   
2. Nach dem Start des Applets "Biege- und dehnsteife ebene Rahmen (FEM)" (und Doppelklick in den Mittelbereich) wird die Zeichenfläche vorbereitet. Für das System mit einer Breite von 2000 mm und einer Höhe von 1000 mm (Werte werden als x-max bzw. y-max eingestellt) wird hier sinnvollerweise mit einer Rasterbreite in x-Richtung von 1000 mm und in y-Richtung von 500 mm gearbeitet, so dass alle markanten Punkte getroffen werden. Dies wird über die Registerkarte "Zeichenfläche" in dem Register links oben erledigt.
   
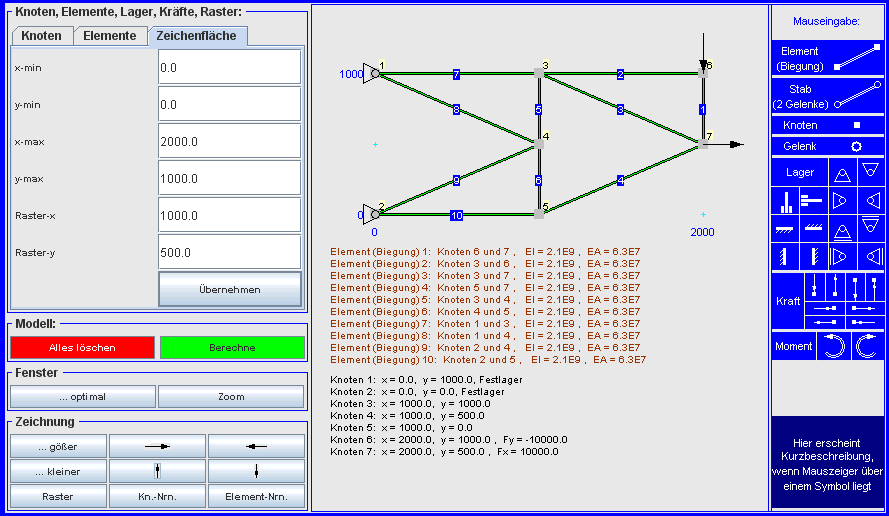
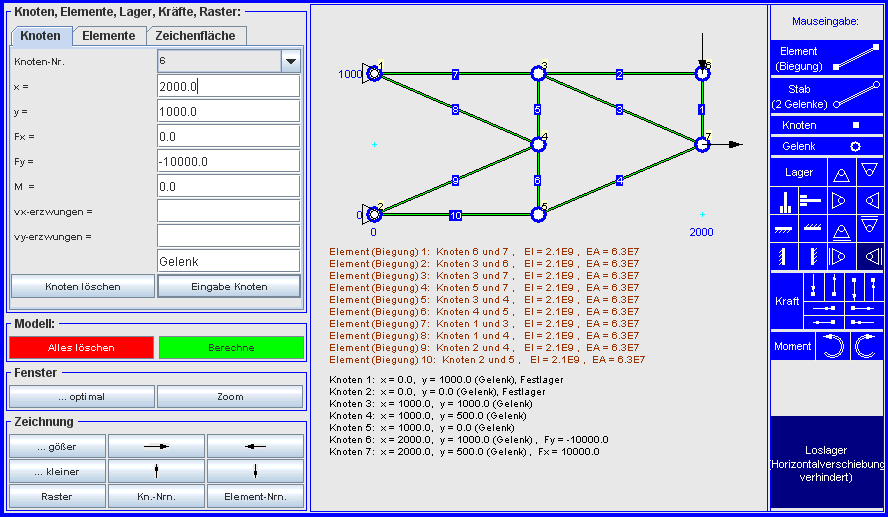
   Danach werden die Knoten, biegesteifen Elemente (nur beim ersten Element müssen EI und EA eingegeben werden, für alle weiteren Elemente werden die Werte automatisch übernommen), Lager und Kräfte eingegeben. Das wird hier nicht detailiert beschrieben, eine ausführliche Beschreibung der Eingabe eines Systems findet man hier. Nach der kompletten Eingabe des Modells sieht der Bildschirm so aus:
   
   
   
   
   
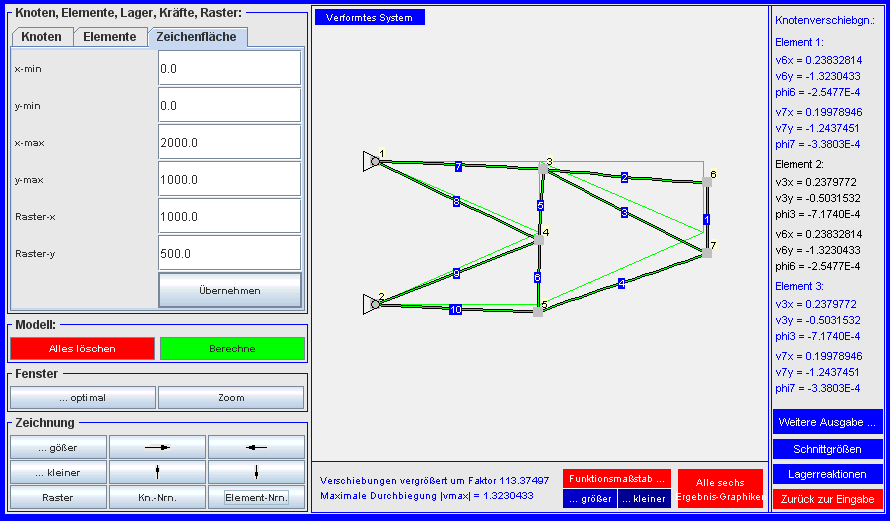
3. Nach Anklicken des grünen Buttons "Berechne" im linken Menü wird die Berechnung gestartet, die Ergebnisse werden in mehreren Graphiken angezeigt, und rechts werden die Knotenverformungen gelistet. Die kleinen Bildchen sind etwas unübersichtlich, dienen aber im Wesentlichen zur Auswahl: Klicken auf das Bildchen "Verformtes System" zeigt diese Graphik groß an. 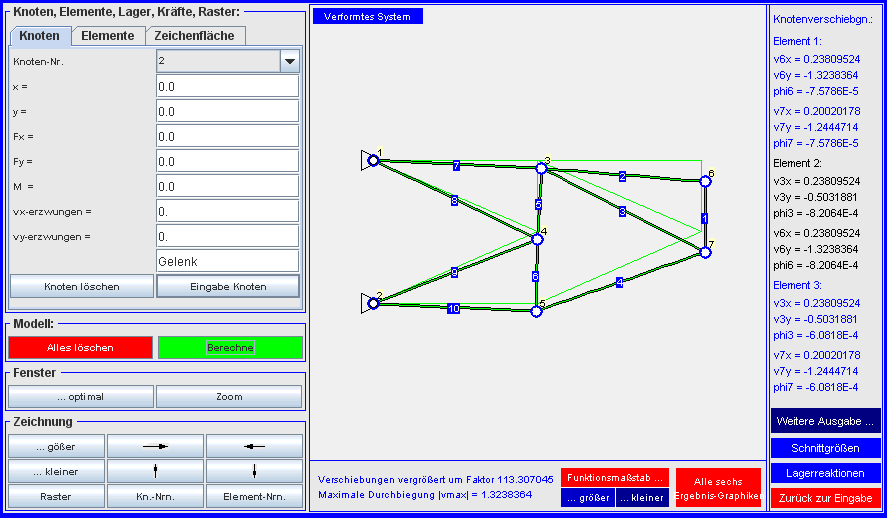In dieser Anzeige sind dann alle Angebote zur Veränderung der Graphik (unten links) verfügbar. Die größte Verformung ist die Vertikalverschiebung des Knotens 6 mit v_max = 1,3230 mm:
   
   
   
   
   
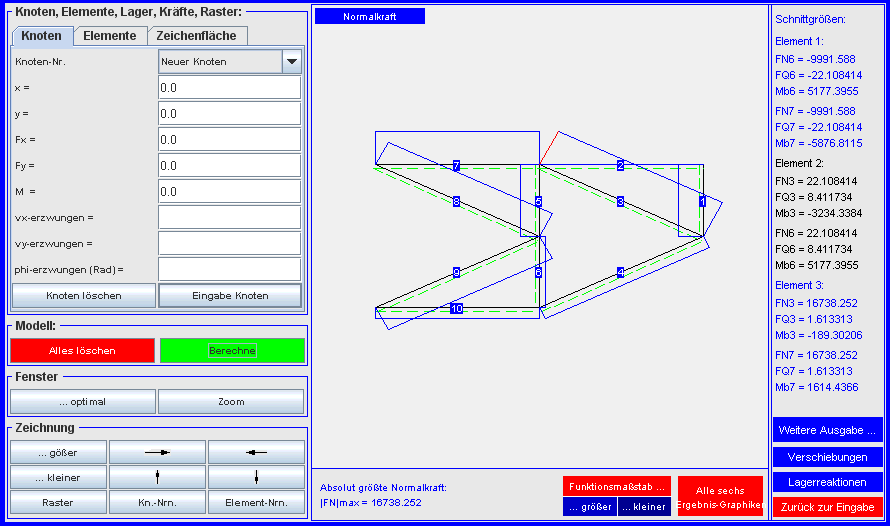
4. Nach Anklicken des roten Buttons "Alle sechs Ergebnis-Graphiken" landet man wieder in der Graphik-Auswahl. Nach Anklicken des Buttons "Schnittgrößen" (rechts unten) werden diese elementweise gelistet, und mann kann sich z. B. die dazu passende Graphik "Normalkraft" anzeigen lassen. Die größte Normalkraft tritt mit 16738 N im Element 3 auf:
   
   
   
   
   
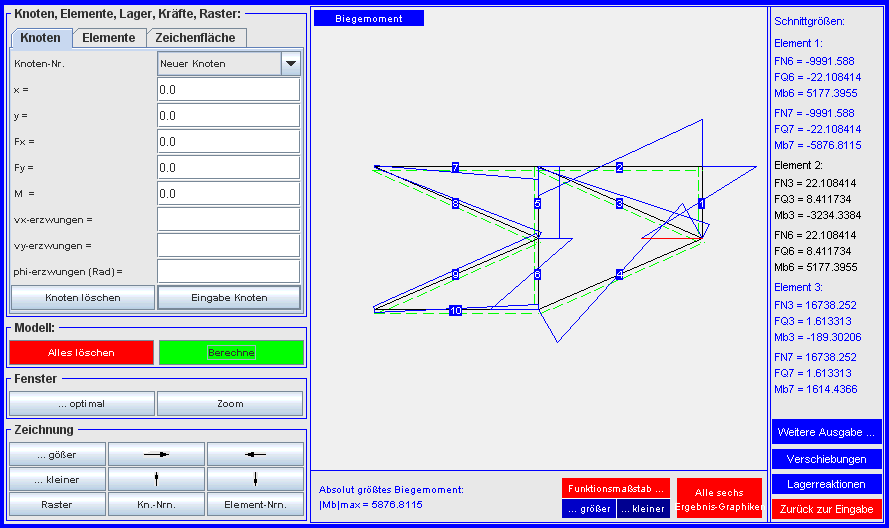
5. Bei biegesteifen Systemen sind die Biegemomente im Allgemeinen die kritischen Schnittgrößen für die Spannungen (zurück über "Alle sechs Ergebnis-Graphiken", dort die Graphik "Biegemoment" auswählen). Das absolut größte Biegemoment tritt mit 5877 Nmm im Element 1 auf:
   
   
   
   
   
6. Über den Button "Zurück zur Eingabe" (ganz unten rechts) kommt man wieder zur Darstellung des Berechnungsmodells, das nun zum "Quasi-Fachwerk" verändert wird, indem alle (biegesteifen) Knoten zu Gelenken gemacht werden (Klicken auf das Angebot "Gelenk" und anschließend auf einen Knoten). Auch die beiden Knoten an den Lagern müssen zu Gelenken gemacht werden, denn die Festlager sind zwar Gelenke, aber die beiden dort angeschlossenen Träger wären sonst untereinander biegesteif verbunden. Nachdem alle 7 Knoten zu Gelenken gemacht wurden, sehen die Graphik und das Protokoll des Systems so aus:
   
   
   
   
   
7. Es wird wieder links der grüne Button "Berechne" angeklickt. Nachfolgend wird das verformte System gezeigt. Die größte Verformung ist die Vertikalverschiebung des Knotens 6 mit v_max = 1,3238 mm:
   
   
   
   
   
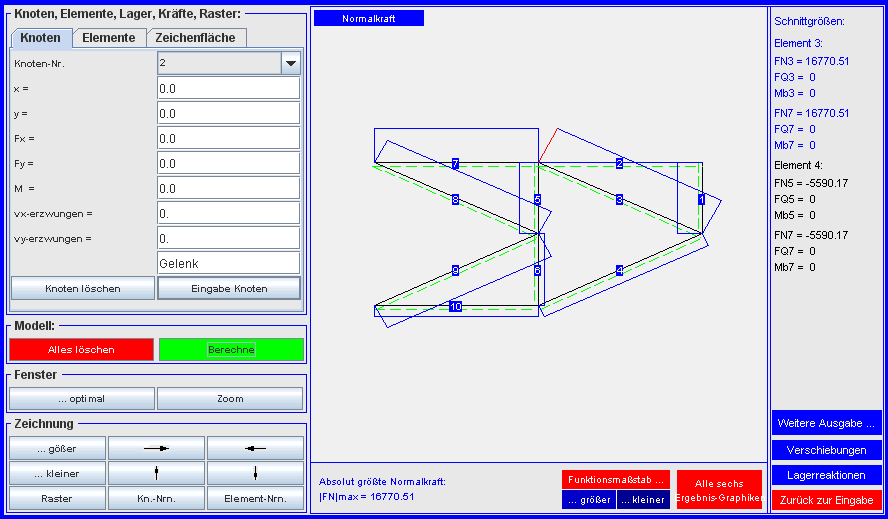
8. Bei den Schnittgrößen ergeben sich erwartungsgemäß nur Normalkräfte (es sind die Stabkräfte des Fachwerks. Die größte Normalkraft findet man auch hier im Element 3 (16771 N):
   
   
   
   
   
9. Vergleich der beiden Rechnungen:
   
   
   • Bei den Verschiebungen sind die Unterschiede marginal: Die maximale Absenkung ergibt sich bei beiden Rechnungen für den Knoten 6 mit v₆ = 1,3230 mm für das biegesteife Tragwerk bzw. v₆ = 1,3238 mm für das ideale Fachwerk.
     
     
   • Auch die Normalkräfte zeigen keine nennenswerten Unterschiede. Die größte Normalkraft (jeweils im Element 3) für das biegesteife Tragwerk hat den Wert F_N,3 = 16738 N, für das Fachwerk ist es die Stabkraft F_S,3 = 16771 N.
     
     
   • Biegemomente treten nur beim biegesteifen Tragwerk auf. Sie machen den Unterschied aus, wobei der Vergleich über die Spannungen geführt werden muss: Die Normalkräfte rufen im Element 3 mit dem Querschnitt A = 300 mm² die Spannungen σ_N,3 = F_N,3/A = 55,8 N/mm² (biegesteifes Tragwerk) bzw. σ_S,3 = F_S,3/A = 55,9 N/mm² (Fachwerk) hervor. Für das biegesteife Tragwerk ergab sich für dieses Element das Biegemoment M_b = 1614 Nmm. Mit dem Widerstandsmoment des Querschnitts W_b = b·h²/6 = 1000 mm³ berechnet man die Biegespannung σ_b,3 = M_b/W_b = 1,61 N/mm², die der Normalkraft-Spannung überlagert werden muss, was nur eine unbedeutende Korrektur ergibt.
     
     Das größte Biegemoment tritt im Element 1 mit 5877 Nmm auf, was auf eine Biegespannung von 5,88 N/mm² führt. Dort ist aber die Normalkraftspannung deutlich kleiner als Normalkraftspannung im Element 3.
     
     Fazit: Die Idealisierung eines Tragwerks dieser Art als ideales Fachwerk ist durchaus gerechtfertigt. Die Abweichungen der Ergebniss bei den Verformungen sind verschwindend gering und liegen bei den Spannungen innerhalb der Grenzen, die bei Praxis-Problemen ohnehin von den Sicherheitsbeiwerten abgedeckt werden.